MILLER INDICES
What are those numbers in parentheses on crystal drawings?
by
Dave Babulski, Ed.D.
("Tips and Trips", Vol. XXXVIII/Nine, September 2009, Pages 10 & 11)
When looking through books on mineralogy, do you ever wonder what those three numbers in parentheses, like this: (100), on crystal faces or in the description of crystals are supposed to represent? In these months Micromount Corner I will try and explain, in simple terms, what those numbers are. We will not go into the mathematics of Miller Indices, but rather take a non-mathematical simple case approach to what can be a rather esoteric complex subject. So let’s get started. Every mineral crystal can be described has having three axes; usually labeled as a, b and c. The hexagonal crystal system has four axes, but we will ignore that for now. To keep our discussion as simple as possible I will limit the discussion to isometric crystals. Figure 1 shows a simple cubic crystal with the three axes labeled as a and a-, b and b- and c and c-. In this crystal system all the axes are equal length. This simplifies the mathematical aspect as we can see that each face of the cube crosses an axis at the same distance. For simplicity sake we will label that distance as1 unit of distance.
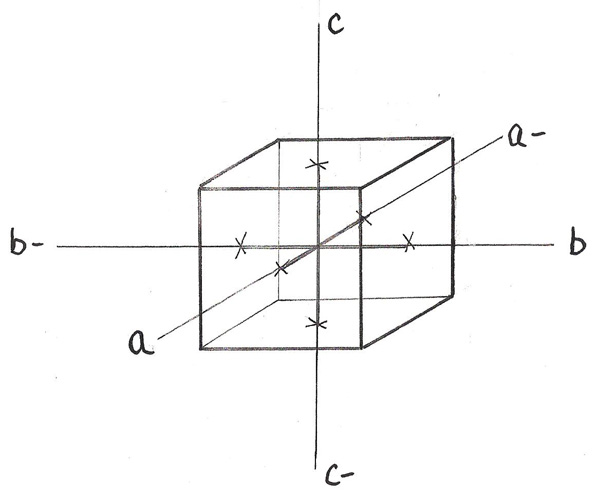
Figure 1
Notice that the “a” axis runs from front to back through the crystal, the “b” axis runs from left to right through the crystal and the “c” axis runs vertically through the crystal. The minus sign on each axis just means it is on the “back side” of the crystal. Let’s look at the top face of our cubic crystal.
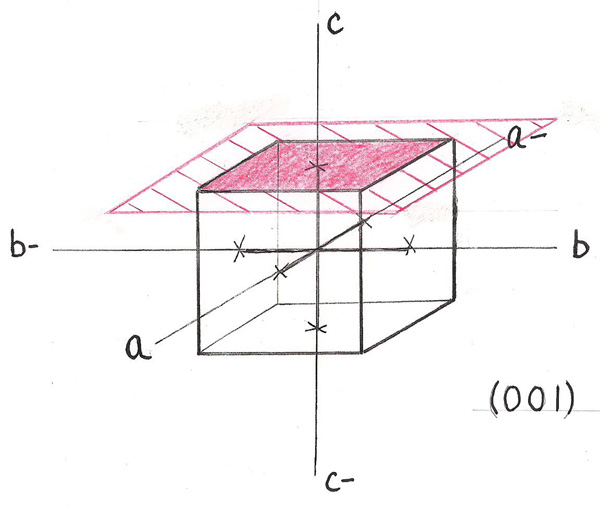
Figure 2
As shown in Figure 2, the top face of our cubic crystal has been shaded in Magenta. Now suppose we extend that face out in every direction a bit as shown by the crosshatched portion. Notice, from figure 2, that this crystal face crosses the “c” axis at 1 unit of distance but remains parallel to the “a” and “b” axes and if run out to infinity would never cross theses axes. Now a tidbit of information: Miller Indices are always listed in terms of the three crystal axes in the form: “a” first, “b” second and “c” third. So we can say that the top crystal face of our cubic crystal cuts the “c” axis at 1 and the “a” and “b” axes at infinity; we can show this symbolically as: ∞ ∞ 1. Well infinity is a rather cumbersome number! So if we take the inverse of these three numbers we get: 0 0 1. It is common practice to put the Miller Indices numbers in parentheses as shown in the bottom right of Figure 2. Let’s look at another example. As shown in Figure – 3 the left hand face of our cubic crystal, shaded in magenta, cuts the “b” axis at 1 unit of distance.

Figure 3
If we extend this crystal face out in every direction, as shown by the cross hatched portion, we see that it remains parallel to the “c” and “a” axes to infinity. So we can show this symbolically as: ∞ 1 ∞. Again, taking the inverse of these numbers we get: 0 1 0 or in common Miller Indices form: (010). The next example shows what happens if a crystal face cuts one of the crystal axes on the back side of the crystal.

Figure 4
As shown in Figure 4, the back crystal face, shaded in magenta, cuts the “a” axis, at 1 unit of distance, on the back side. Note that the “a” axis is labeled with a minus sign to indicate it is the back side of the “a” axis. If we extend this crystal face out in every direction, as shown by the cross hatched portion, we see that it remains parallel to the “b” and “c” axes to infinity. So we can show this symbolically as: -1 ∞ ∞. Now as before, if we take the inverse of these numbers we get: -1 0 0. In Miller Indices practice, the negative is indicated by a bar over the number 1, as shown in the lower left of Figure 4. This is pronounced as ”bar one”. Suppose, instead of a face of the cube we have a corner face as shown, shaded in magenta, in Figure 5.
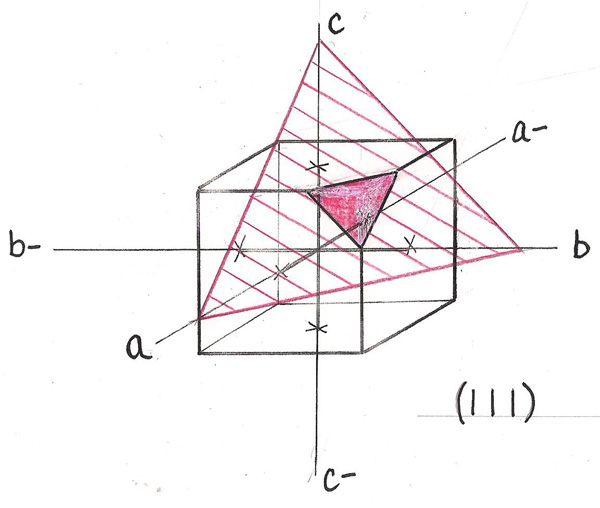
Figure 5
If we extend the edges of this triangular crystal face out in every direction we see it cuts all three axes at the same distance of 2 units. We can represent this symbolically as: 2 2 2. Since the idea is to keep the numbers as small as possible we can divide through by the common factor of 2 to get: 1 1 1. In Miller Indices format this would become (111), as shown in the lower right of Figure – 5. Figure – 6 shows our cubic crystal with all the faces labeled with Miller Indices.
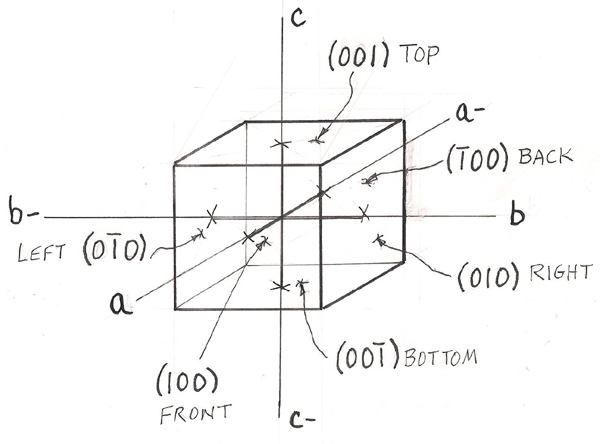
Figure 6
Notice in Figure 6 that the top and bottom faces are inverse of each other as are the right and left faces and front and back faces. The subject of crystallography is a very complex one. I have tried to explain in simple terms about the Miller Indices for crystals. At this point hopefully you have a better idea of what those numbers in parentheses are in crystal drawings. From a micromounter perspective it is often useful, when describing a crystal seen through the microscope, to use Miller Indices notation. If you would like to pursue this subject in more detail I have listed some useful references and additional reading below.
REFERENCES: Mason, B and Berry, L.G., Elements of Mineralogy, W.H. Freeman and Co., San Francisco, Pages 20 – 23 Smith, J.R., A Guide to Understanding Crystallography, Self Published; Jennie R. Smith, 1991, Pages 66 – 72 Dana, E.S. and Ford, W.E., Dana’s textbook of Mineralogy, John Wiley and Sons, New York, 1966, Pages 43 – 67
http://www.tulane.edu/~sanelson/eens211/axial_ratios_parameters_miller_indices.htm
http://www.chem.qmul.ac.uk/surfaces/scc/scat1_1b.htm http://www.gly.uga.edu/schroeder/geol6550/millerindices.html http://www.encyclopedia.com/doc/1O13-Millerindices.html
Until next time, may all your skies be blue and all your vugs be crystal filled.

Figure 1
Notice that the “a” axis runs from front to back through the crystal, the “b” axis runs from left to right through the crystal and the “c” axis runs vertically through the crystal. The minus sign on each axis just means it is on the “back side” of the crystal. Let’s look at the top face of our cubic crystal.

Figure 2
As shown in Figure 2, the top face of our cubic crystal has been shaded in Magenta. Now suppose we extend that face out in every direction a bit as shown by the crosshatched portion. Notice, from figure 2, that this crystal face crosses the “c” axis at 1 unit of distance but remains parallel to the “a” and “b” axes and if run out to infinity would never cross theses axes. Now a tidbit of information: Miller Indices are always listed in terms of the three crystal axes in the form: “a” first, “b” second and “c” third. So we can say that the top crystal face of our cubic crystal cuts the “c” axis at 1 and the “a” and “b” axes at infinity; we can show this symbolically as: ∞ ∞ 1. Well infinity is a rather cumbersome number! So if we take the inverse of these three numbers we get: 0 0 1. It is common practice to put the Miller Indices numbers in parentheses as shown in the bottom right of Figure 2. Let’s look at another example. As shown in Figure – 3 the left hand face of our cubic crystal, shaded in magenta, cuts the “b” axis at 1 unit of distance.

Figure 3
If we extend this crystal face out in every direction, as shown by the cross hatched portion, we see that it remains parallel to the “c” and “a” axes to infinity. So we can show this symbolically as: ∞ 1 ∞. Again, taking the inverse of these numbers we get: 0 1 0 or in common Miller Indices form: (010). The next example shows what happens if a crystal face cuts one of the crystal axes on the back side of the crystal.

Figure 4
As shown in Figure 4, the back crystal face, shaded in magenta, cuts the “a” axis, at 1 unit of distance, on the back side. Note that the “a” axis is labeled with a minus sign to indicate it is the back side of the “a” axis. If we extend this crystal face out in every direction, as shown by the cross hatched portion, we see that it remains parallel to the “b” and “c” axes to infinity. So we can show this symbolically as: -1 ∞ ∞. Now as before, if we take the inverse of these numbers we get: -1 0 0. In Miller Indices practice, the negative is indicated by a bar over the number 1, as shown in the lower left of Figure 4. This is pronounced as ”bar one”. Suppose, instead of a face of the cube we have a corner face as shown, shaded in magenta, in Figure 5.

Figure 5
If we extend the edges of this triangular crystal face out in every direction we see it cuts all three axes at the same distance of 2 units. We can represent this symbolically as: 2 2 2. Since the idea is to keep the numbers as small as possible we can divide through by the common factor of 2 to get: 1 1 1. In Miller Indices format this would become (111), as shown in the lower right of Figure – 5. Figure – 6 shows our cubic crystal with all the faces labeled with Miller Indices.

Figure 6
Notice in Figure 6 that the top and bottom faces are inverse of each other as are the right and left faces and front and back faces. The subject of crystallography is a very complex one. I have tried to explain in simple terms about the Miller Indices for crystals. At this point hopefully you have a better idea of what those numbers in parentheses are in crystal drawings. From a micromounter perspective it is often useful, when describing a crystal seen through the microscope, to use Miller Indices notation. If you would like to pursue this subject in more detail I have listed some useful references and additional reading below.
REFERENCES: Mason, B and Berry, L.G., Elements of Mineralogy, W.H. Freeman and Co., San Francisco, Pages 20 – 23 Smith, J.R., A Guide to Understanding Crystallography, Self Published; Jennie R. Smith, 1991, Pages 66 – 72 Dana, E.S. and Ford, W.E., Dana’s textbook of Mineralogy, John Wiley and Sons, New York, 1966, Pages 43 – 67
http://www.tulane.edu/~sanelson/eens211/axial_ratios_parameters_miller_indices.htm
http://www.chem.qmul.ac.uk/surfaces/scc/scat1_1b.htm http://www.gly.uga.edu/schroeder/geol6550/millerindices.html http://www.encyclopedia.com/doc/1O13-Millerindices.html
Until next time, may all your skies be blue and all your vugs be crystal filled.

Copyright © Georgia Mineral Society, Inc.
